Animated GIFs on random topics. Copy as is. Browse and have fun.
For the video tutorials, go to the Home page.
Curvature
In curved space, try to lay out a perfect grid of meter sticks. You can’t. You end up with extra “pixels” that don’t fit. Either shorten some sticks, or let them bulge out in the third dimension.
A 2d closed surface can be viewed at embedded in 3d, or as a distorted disk in 2d (Feynman’s hot plate):

Geodesic: traced by a cart on a 2d spherical surface embedded in 3d:

Geodesic: traced by cart on Feynman’s hot plate, where the wheel sizes (or speeds) vary:

In 3d, a grid of rods make voxels (3d pixels)…:

…and in 4d, a grid of rods (including time rods) make hypervoxels (4d pixels):

Curvature of time. Just like the space dimensions deform or buckle, time stretches in 4d “voxels.” Where the copper “time-stick” is long, clocks run slow.

There’s a conspiracy of nature: When everything runs in slow motion — clocks, your brain, your muscles… — you cannot tell:

Black holes
Schwarzschild spacetime. Increase the mass, spacetime curves:

Static (Schwarzschild) black hole. Particle falls, seems to freeze, then happens to bounce on something (mirror, quantum fluctuation…)

Black holes don’t “suck” in matter any more than a star of the same mass. Orbits of particles are the same. In fact, black holes are less likely to swallow a particle, because it’s smaller, and most particles fly right past the black hole. You need a head-on collision to get destroyed, and for black holes, being very small, that’s rare:

Rotating (Kerr) black hole. Particle falls, is frame-dragged, orbits an infinite number of times before reaching the event horizon:

At the event horizon, light cones tip over, so an outside cannot say: “the falling thing has crossed the horizon”:

At the event horizon, clocks slow to zero. As with the Shapiro delay, you could bounce just outside the event horizon, and reappear after a trillion years:

When a black hole evaporates (via Hawking radiation), you cannot fall across the event horizon (more details here):

Slow light
For the same measured distance, light takes different time to bounce and return. This Shapiro delay can be arbitrarily large when bouncing close to the event horizon of a black hole. Taylor and Wheeler refer to this as “slow light”:

Prism: light bends toward slower light. Half of the light flash (“wave front”) enters the prism first, slowing down, turning the light flash toward the prism:

Light bends toward slower light. Here, we cannot make a square with 90 degree angles:

Measuring the local speed of light always gives c, because your measurement equipment slows along with light.
Wormholes
Travel the quick way, through a wormhole:

Build a worm hole by connecting two “mouths” in the embedding dimension:

Morris-Thorne wormhole. Step into one mouth, step out the other (along yellow rods):

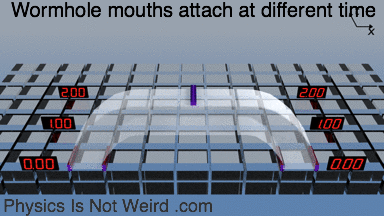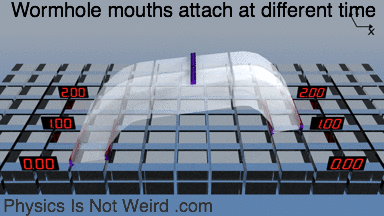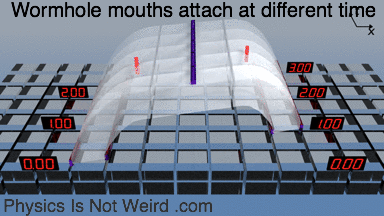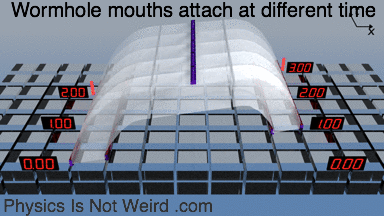
The two wormhole mouths can be attached at different times:

Same skewed attachment with the t coordinate visualized. You can the make a time machine (more here).
Cosmology
The universe looks the same from everywhere, even when it’s closed:

A closed universe is not infinite. Go straight, and you loop back to where you started, just like on planet Earth’s surface.

A closed universe is not infinite. It could be like the surface of the Earth, closing back on itself (in an embedding dimension), or it could be a hot plate (see Feynman’s lecture), where spacetime distorts just so that it behaves like a spherical surface. You get different boundary conditions for a path that hits the edge head on:

In an open (infinite) universe, turn the curvature up and down:

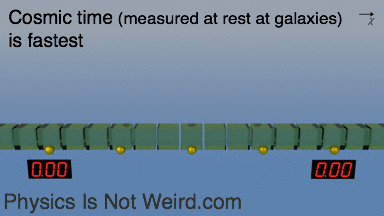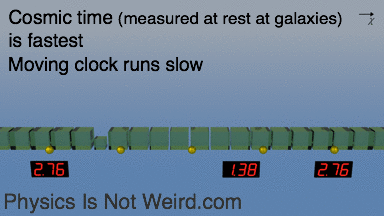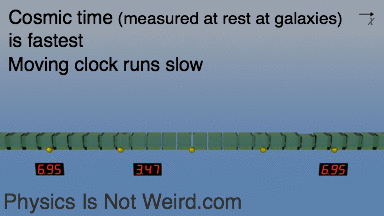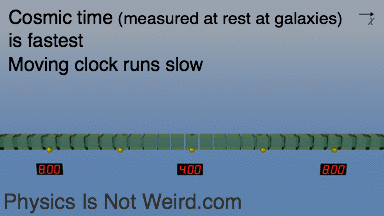
With expansion, space is added between galaxies that sit still. Cosmic time is measured “at rest” and runs the fastest. A moving clock (for example one at fixed distance during expansion) shows less time:
With expansion, matter and radiation is diluted. Dark-energy density stays the same:

With matter (yellow dots) the universe decelerates. With enough dark energy (red dots), the universe accelerates:

Early inflation, before the other eras:
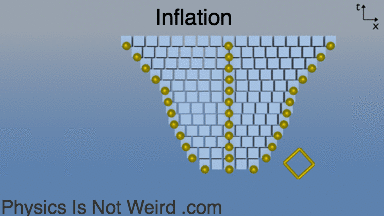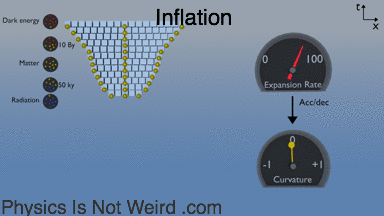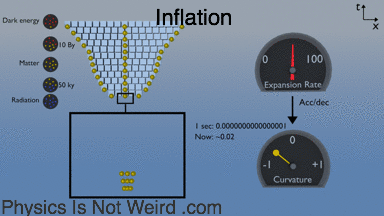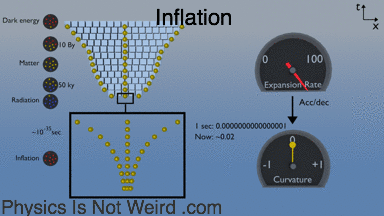
Gravitational wave: A cyclic expansion–contraction of space:

The expansion rate of the universe is measured in [1/s], not [m/s]. It’s not a speed. So please don’t say that “it’s expanding faster than light.” However, the distance [m] between two galaxies changes with time [m/s], so you can call this a recession speed. The further apart, the higher the recession speed. You can always find two points receding faster than light, even when expansion is slow:
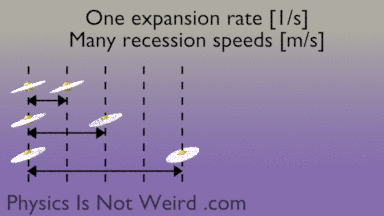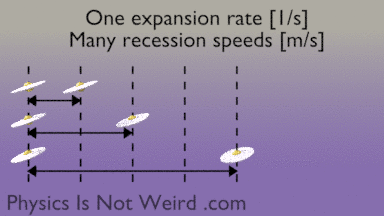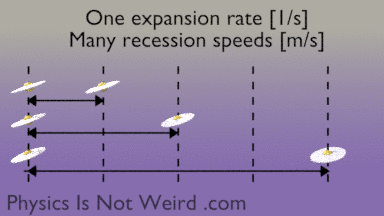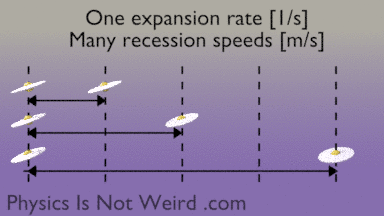
During 13 billion years, a galaxy can recede by much more than 13 billion light-years, because of expansion. A photon emitted by the receding galaxy may initially be “expanded away,” then eventually catch up and reach us.

Special Relativity
Video tutorial here.
The three effects at high speed: length contraction, time dilation, desynchronization:
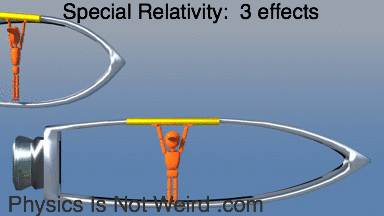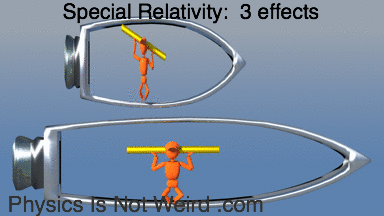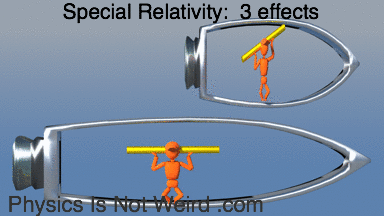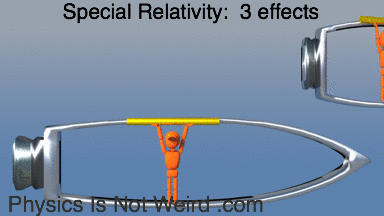
Synchronize clocks while moving: Method 1. Flash light halfway between clocks, reset clocks to zero when they detect the flash. Fails on moving ship). because flash takes longer to catch up to front clock:

Synchronize clocks while moving: Method 2. Synchronize clocks at same location, then move them apart. Fails identically on moving ship, because front clock moves faster, runs slower:

Conspiracy of nature: Moving, contracted ship measures at-rest, long ship to be contracted:

Conspiracy of nature: Moving ship has slow clocks, but measures at-rest fast clocks to be slow! Why? Because moving clocks are desynchronized:
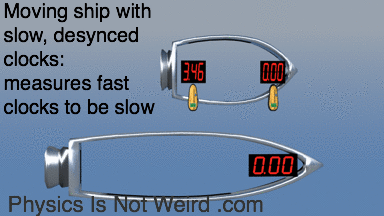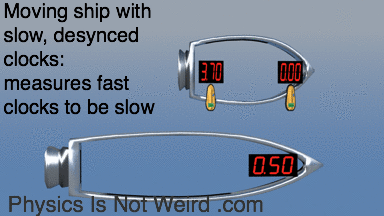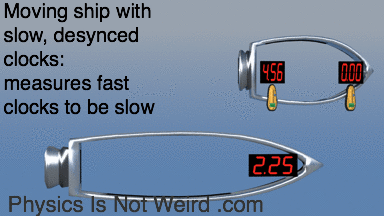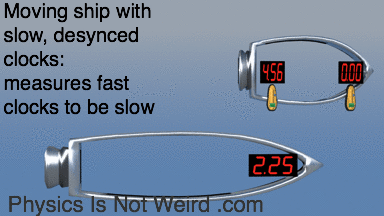
Paradoxes evaporate with you remember that it’s all about measurements, by an observer that may be moving, not about some global, external POV:

Conspiracy of nature: When you and your meter stick both contract, you cannot tell (locally):
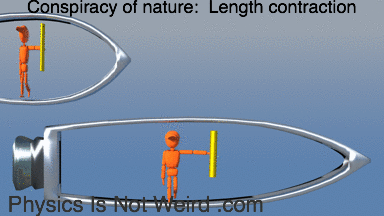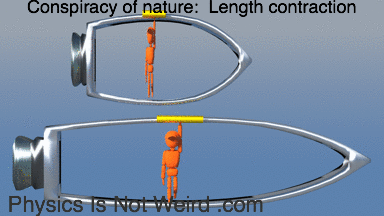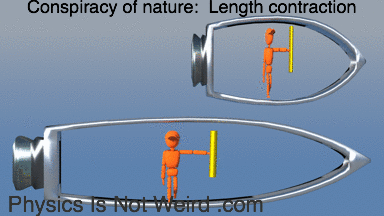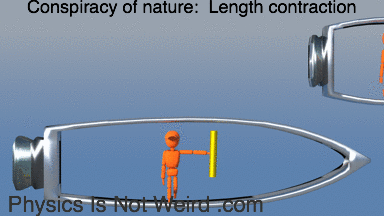
Conspiracy of nature: When you and your clocks run in slow motion, you cannot tell (locally). Also note tilted rod (clock desynchronization):
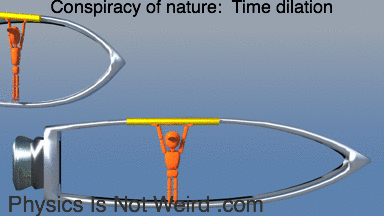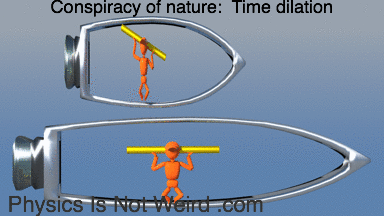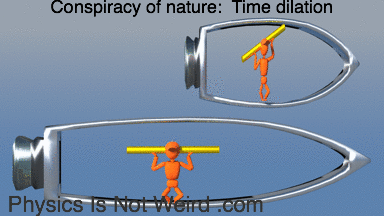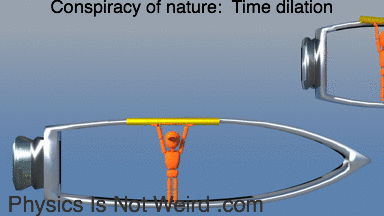
For a spinning ring, you get time dilation. For length contraction, it’s the instantaneous velocity that matters. The spokes don’t get shorter, but the yellow rods do, so you get gaps:

For the spinning ring, you cannot synchronize clocks all the way around (blue light flashes propagate):

Breathers (sine-Gordon)
A non-linear string can “trap” the energy of a disturbance. Below, the top string oscillates between kinetic and potential energy, in one location, like a particle at rest. (The boring linear string, bottom: waves rush off at the speed of the medium, c):

Sine-Gordon breathers, like particles, obey Special Relativity: they contract, the oscillations dilate in time, and the front lags behind the rear. Also, the total energy, E = T+U of the non-linear string, increases with a -factor:
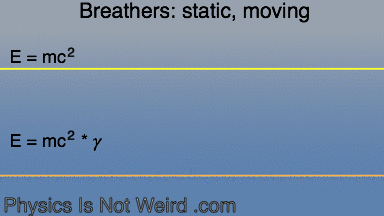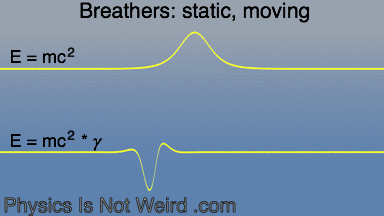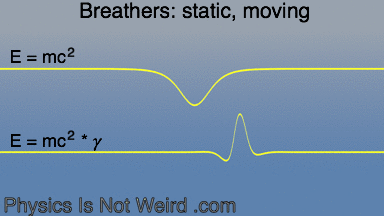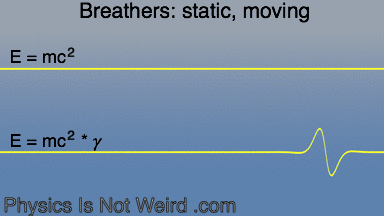
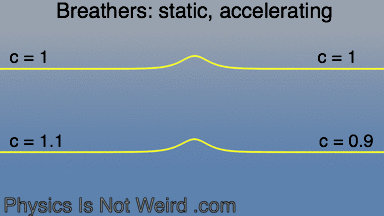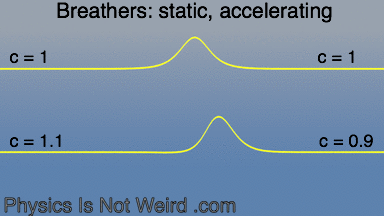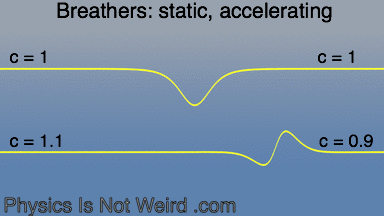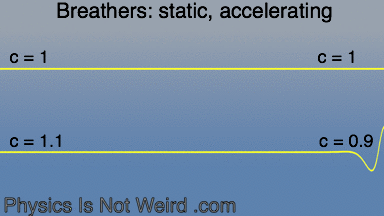
Sine-Gordon breathers, like particles, obey General Relativity in one respect: they accelerates toward where c (the speed of the medium) is smaller:
Particles
Binding energies: the more tightly bound, the more energy needed to remove. For quarks, so much energy is input that new quarks are created, bonding with the remnants: